2015-11-08

KUPC2015復習記(A~G)

KUPC2015にオンサイトで参加しました！KUPCに参加すること自体初で、コンテストにオンサイトで参加するのはindeedなう以外で初めてです。

kupc2015.contest.atcoder.jp

結果は以下の通りで不甲斐ない結果でした。もうちょい通したかったなあ..特に最後の一時間でFが通せなかったのが一番悔しかったです。 f:id:Tawara:20151106143825p:plain 参加記書こうと思いつつ気付けば二週間経ってたので、少し詳しく復習記事を書くことにしました。以降の記事は色々考えたこととかソースコードが載ってるので大分長くなってます。

A - 東京都

問題文

A: 東京都 - 京都大学プログラミングコンテスト2015 | AtCoder

解法

一瞬迷ったんですが、前から順番に見て'kyoto'か'tokyo'があれば切り出すのを繰り返せば問題ないだろうということで提出しました。

実装

indexとか使えばもっと簡単に書けるかもしれない。

T = int(raw_input())
for i in xrange(T):
    S = raw_input()
    sl = len(S)
    inc = cnt = 0
    while inc < sl-4:
        if S[inc:inc+5] == 'tokyo' or S[inc:inc+5] == 'kyoto':
            cnt += 1
            inc += 5
        else:
            inc += 1
    print cnt

B - GUARDIANS

問題文

B: GUARDIANS - 京都大学プログラミングコンテスト2015 | AtCoder

解法

方眼紙にひたすら書く。

ってのが参加時の僕の行動です。最終的に鎖頭を５匹配置して下一行を侵入者が通るようにしました。解説で出された４匹解答は衝撃的でしたね。

ちなみに、４匹の鎖頭の配置の仕方は $_{100}C_4 = 3921225 \fallingdotseq 4.0 * 10^6$ なので、それら全てに対して探索を行っても間に合うそうです。

実装

これ実装やない、ただの出力や。

print ".........."
print ".........."
print "..C......."
print ".........."
print ".........."
print ".........."
print "..CC..CC.."
print ".........."
print ".........."
print ".........."

C - 最短経路

問題文

C: 最短経路 - 京都大学プログラミングコンテスト2015 | AtCoder

解法

エッジの数が指定されてないので、とりあえず与えられた最短距離を持つエッジを全部張ったグラフを考えます。このときに問題が発生するのは、頂点 $i$ から別の頂点を経由して頂点 $j$ に行く経路の長さが、頂点 $i$ から頂点 $j$ に直接行くよりも短い場合です。このような場合は条件を満たす有向グラフが存在しないことになります。

f:id:Tawara:20151106172034p:plain

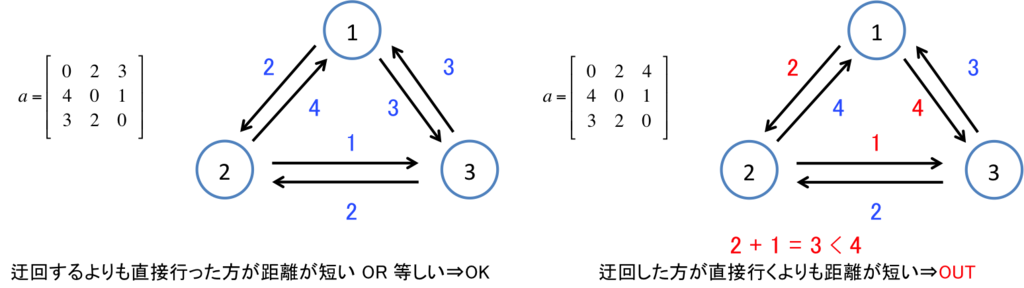
要は与えられた最短距離から全頂点対の最短距離を計算し直して、与えられた最短距離より短くなっているところがあったらアウトです。頂点数 $N$ の制約は( $1 \leq N \leq 30$ ) と小さいので、 $O(N^3)$ のワーシャルフロイドの出番ですね！

あと、与えられる最短距離の行列の対角成分は当然0になると思いがちですが、今回はそうでないものも含まれてるので弾く必要があります。単純有向グラフの定義では自己辺は存在しないので、そのために入れたんですかね？

実装

参加時は念のためにC++で通したんですが、計算量が $O(TN^3)$ なので冷静に考えるとpythonでも普通に通りますね。

問題設定では $a_{ij} = -1$ の場合に頂点 $i$ から頂点 $j$ への経路が存在しないのですが、ワーシャルフロイドで計算して行く都合上MAX( = $10^7$ )に書き換えました。いずれかの $(i.j)$ に対して $d_{ij}$ が $a_{ij}$ より小さければ有向グラフが存在しないので"NO"を出力します。

最近any()とall()の存在を知ったので使ってみました。

T = int(raw_input())
MAX = 10000000
for i in xrange(T):
    N = int(raw_input())
    a = [map(int,raw_input().split()) for i in xrange(N)]
    d = [[MAX]*N for i in xrange(N)]
    for i in xrange(N):
        for j in xrange(N):
            if a[i][j] == -1:
                a[i][j] = MAX
            d[i][j] = 0 if i == j else a[i][j]
    for k in xrange(N):
        for i in xrange(N):
            for j in xrange(N):
                d[i][j] = min(d[i][j],d[i][k]+d[k][j])
    print "NO" if any(d[i][j] < a[i][j] for i in xrange(N) for j in xrange(N)) else "YES"

D - 高橋くんの旅行

問題文

D: 高橋君の旅行 - 京都大学プログラミングコンテスト2015 | AtCoder

参加時に取り組んだけど解けませんでした(その１)。解法が思いつかず、部分点だけとって放置してました。

部分点解法

問題文見たとき単純なDPで行けるかな？って思ったんですが、 $N$ の制約が $1 \leq N \leq 10^5$ なため相当厳しい..。i日目に到達できる都市の番号が最大でもi+1であることを勘案しても、計算量が $N^2/2$ 位になるのでC++でも無理でした。部分点の制約は $1 \leq N \leq 10^3$ なのでこの方法で部分点が取れます。

実装

int main(){
    int N;
    LL ans = 0;
    VLL dp,A,B;
    cin >> N;
    A.resize(N); B.resize(N);
    rep(i,N) cin >> A[i];
    rep(i,N) cin >> B[i];
    dp = VLL(N+1,-1);
    dp[0] = 0;
    rep(i,N){
        for(int j = i+1; j >= 0; j--){
            if (dp[j] >= 0){
                dp[j+1] = max(dp[j+1],dp[j]+A[j]);
                dp[j] = max(dp[j],dp[j]+B[j]);
            }
        }
    }
    rep(i,N+1) ans = max(ans,dp[i]);
    cout << ans << endl;
    return 0;
}

満点解法

解説によると、ポイントは「いずれのiについても $B_i \geq 0$ が成り立つ」ということだそうです。更にポイントとして、都市 $i$ での滞在で得られる $B_i$ は何日目であろうと変化しないこと、都市 $i$ から都市 $i+1$ への移動は一回しか起こらない、ということが挙げられそう。

解法としては、最後に居る都市 $i$ さえ決めてしまえば $B_j$ が最大となる都市 $j$ $(1\leq j \leq i)$ に出来るだけ滞在することでお金を最大に出来ます。言われてみればなるほどって感じですね。先に都市を決めるって発想に至れなかった..。これを各 $i$ について求めてしまえば、その最大値が答えになります。

ただし、条件として「いずれの日にも所持金が負になってはいけない」というのがあるので、都市 $i$ を決めたら所持金が負にならずに $i$ に到達できる最小の日数を求め、残りの日数は $B_j$ が最大となる都市 $j (1\leq j \leq i)$ にずっと滞在するという流れになります。

都市 $i$ に最小日数で到達するということは、都市 $i-1$ に最小日数で到達してから出来るだけ少ない日数で都市 $i-1$ から都市 $i$ への移動を行うということ。(都市 $i-1$ に最小日数で到達したときの所持金 $+ A_i$ ) が負でなければ即座に移動が行えますが、そうでない場合は $B_j$ が最大となる都市 $j$ $(1 \leq j \leq i-1)$ に滞在しつづけることで、最小の日数で移動可能な状態にすることができます。

実装

dayは都市 $i$ へ到達する最小日数, moneyはその時点での所持金です。for文の前半で最後に居る都市が $i$ であるときの所持金の最大値 ${ans}_i$ を求め、後半でdayとmoneyを更新してます。

N = int(raw_input())
A = map(int,raw_input().split())
B = map(int,raw_input().split())
ans = [0]*(N+1)
day = money = 0
maxB = B[0]
for i in xrange(N):
    if day > N:
        break
    maxB = max(maxB,B[i])
    ans[i] = money + maxB*(N-day)
    day += 1
    money += A[i]
    while money < 0 and day <= N:
        day += 1
        money += maxB
else:
    ans[N] = money
print max(ans)

E - マッサージチェア2015

問題文

E: マッサージチェア2015 - 京都大学プログラミングコンテスト2015 | AtCoder

参加時に取り組んだけど解けませんでした(その２)。普通の長方形と正方形の二パターンしか想定してなかったんですが（↓みたいなやつ）、ほぼ正方形といってもいい長方形だと結果が変わるみたいです。もっと色々考察したり試したりすべきですね。

f:id:Tawara:20151107013115p:plain

解法

厳密な証明が出来る訳じゃないんですが、概ね以下のように考えると納得できそう？ ※横の方が長い(or縦と等しい)長方形を想定

三角形ABCが長方形（談話室）の内部にあるなら、内接させた方が大きい三角形ができる。長方形の内部に三角形ABCがある（または、頂点のうち少なくとも一つが内部にある）場合、図のようにすれば辺の最小値を大きく出来ます。
三角形ABCのいずれの頂点も長方形の角頂点(角)に無い場合、少なくとも一点を角に移動させると大きい三角形ができる。あんまり厳密ではないですが、いずれの頂点も長方形の角に無い場合は図の3パターンなので言えそう。一番短い辺の端点のうちどちらかを動かせば辺の最小値を大きく出来ます。
長方形の一つの辺に三角形の二つの頂点がありかつ、少なくとも一方がその辺を内分している場合、二頂点のどちらかを動かせばより大きな三角形ができる。これも怪しいけど言えそう。
- [左] 二頂点に内分されている辺の対辺上にもう一点がある場合。これは図の通りに動かせば三角形の辺の最小値を大きく出来ます。
- [中央、右] 二頂点に内分されている辺の隣接した辺にもう一点がある場合。この場合は、同じ辺にある二頂点(A,B)のうち三つ目の頂点から遠い方を動かすと三角形の辺の最小値を大きく出来ます。ただし、右のような場合は最初からACが最小なので、最小値を変えずに点を移動させることになります。
三角形ABCが長方形に内接しているとき、一つの辺を固定すると残りの二辺を等しくすれば辺の最小値が最大になる。固定する辺の長さが小さい場合は二等辺三角形でなくても良い場合がありますが、図のように、固定する二頂点を長方形の短い方の対辺の組に置けば二等辺三角形が最適です。

以上のことを考えると、頂点の一つは角に固定出来ます。最後に述べたことから、頂点をもう一つ固定すれば自動的に最後の点の最適な位置が分かるので、二つ目の頂点で探索を行えば解けます。一番下の図で言うとCの位置を探索しますが、Cの最適な位置が辺の端点でない場合は、三角形ABCの辺の最小値は以下のグラフのように上に凸になるはずです(※形がこんな曲線になるかはわかりません)。 f:id:Tawara:20151107041525p:plain 上に凸ということで、たまにしか使わない三分探索を使う機会がやって参りました。

実装

Bを(0,0)に、Cを(w, mid)に固定したとき、Aの最適な位置は

( $\frac{mid^2 - 2mid*h + w^2}{2w},h$ )

です。BCの中点の垂直二等分線と長方形の上の辺の交点なので式を立てれば求まります。このx座標、めっちゃ因数分解出来そうな形してるのに惜しい..

from math import sqrt
lb = 10**(-7)
def side_min(w,h,mid):
    return min(w**2 + mid**2, ((mid**2 - 2*mid*h + w**2)/(2.*w))**2 + h**2)

T = int(raw_input())
for i in xrange(T):
    H,W = map(int,raw_input().split())
    w = max(H,W)
    h = min(H,W)
    l = 0; r = h
    while r-l > lb:
        lmid = (2*l + r) / 3.
        rmid = (l + 2*r) / 3.
        lmin = side_min(w,h,lmid)
        rmin = side_min(w,h,rmid)
        if lmin >= rmin:
            r = rmid
        else:
            l = lmid
    print sqrt(lmin)

図形の辺ってsideで合ってるんですかね？

想定解法

解説によると、三角形ABCの辺の最小値が最大になるときに長方形の角にある頂点が一つだけの場合、三角形ABCは正方形になるらしい..正直なんでか分かりません。この事実を利用すると二分探索で解を求めることができ、更に言うと $O(1)$ で答えを出すことも可能だそうです。

F - 逆ポーランド記法

問題文

F: 逆ポーランド記法 - 京都大学プログラミングコンテスト2015 | AtCoder

参加時に取り組んだけど解けませんでした(その３)。この問題は最後らへんずっと考えてて、方針は合ってたっぽいのに実装がおかしくて通らないという非常に悔しい結果でした。

解法

解説聞いて感動したのが、構文木で考えるとめっちゃわかりやすいということ。問題自体が構文解析っぽいし、解いてるときに「演算子の階層の深さ」とか考えてたんだからむしろ木構造は思いついてしかるべきですよね。思い至らなかったのがとても悔しい。

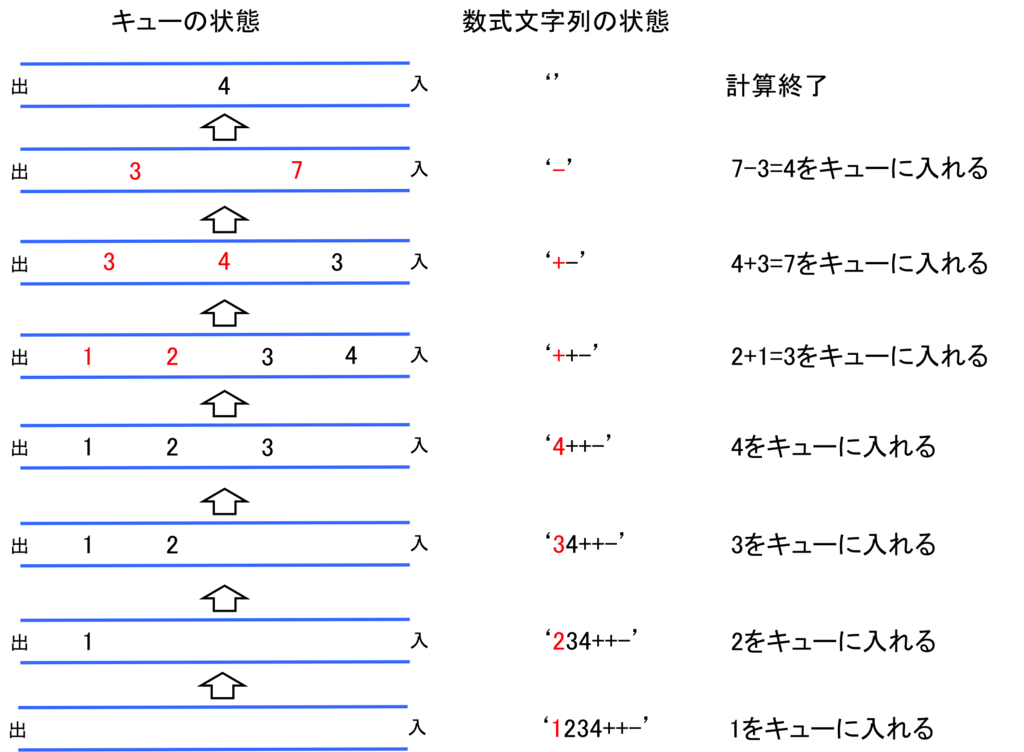
たとえば数式"(4+3)-(2+1)"木構造で表すと、以下のようになります。 f:id:Tawara:20151107140337p:plain この数式を評価する場合、演算子を評価する際にはその左辺(左の子)と右辺(右の子)が全て評価し終わっている必要があり、その順序によって記法が変わります。

逆ポーランド記法の順番 "43+21+-" を見ると、木を左からdfsして葉(または子が既に並べられている節点)から並べています。スタックで処理すると、演算子の左辺の評価値をスタックの奥に追いやったまま右辺の評価を行えるからうまく行くみたいです。

一方キューで処理しようと思うと、演算子で評価した結果がキューの一番後ろに入ってしまうので同じ順番では無理です。ぱっと思いつかないんですが、実は計算の過程を終わりから見て行けばどういう順番になっているがすぐにかわかります。

f:id:Tawara:20151108004433p:plain

同様のことをスタックでもやるとちゃんと逆ポーランド記法の数式文字列が出ますが割愛。

導かれたキューで処理する場合の順番は、木構造を右からbfsして葉(または子が既に並べられている節点)から並べていることが分かります。よって解法としては、逆ポーランド記法から構文木を形成して、深いノードのうち右から順に並べて行けばよいです。

実装

一旦木を作ってしまい、そのあと深いかつ右にあるもの順で並べて行きます。木構造はクラスとかで作るのも可能ですが、セグメントツリーみたいに配列を用意してkの左の子の添字が2k+1、右の子の添字が2k+2になる定番のやり方が楽(このインデックスの仕方って名前ありましたっけ？)。こうすると並べるときに添字の大きい方から並べるだけで済むのでめっちゃ楽です。ただし数式の構文木は平衡木になっているとは限らないので（配列を本当に用意すると余裕でTLEしました）、代わりにディクショナリを使って必要な部分だけ用意するようにしています。

dfsで書いてますが、bfsの方が簡単に書けるらしいです。逆ポーランド記法は一番後ろから読んで行くと木構造が分かりやすいので処理も後ろから行っています。

A = list(raw_input()[::-1])
N = len(A)
tree = dict()
def make_tree(h,pos):
    if pos >= N:
        return
    tree[h] = A[pos]
    if not A[pos].isdigit():
        pos = make_tree(h*2+2,pos+1)
        pos = make_tree(h*2+1,pos+1)
    return pos
make_tree(0,0)
print "".join(tree[k] for k in sorted(tree.keys(), reverse = True))

けっこう綺麗に書けたので個人的には嬉しい。

G - ケンドー

問題文

G: ケンドー - 京都大学プログラミングコンテスト2015 | AtCoder

参加時には読んだけどよくわからなくてH解こうとしたりしてました(そして無理でした)。プロから言わせると典型問題らしい..。

解説では、「 $B_N$ から順に対戦相手を決めて行けばよい」って言われてそれには納得したんですが、それを高速で実現する為にはどうするかってのがよくわかってませんでした。この問題は自力で解くのが難しかったので、他の方の参加記等に~~パクリに~~ヒントをもらいに行くと、

$B_N$ から決めて行けば、後はBIT使えばOK
FenWick Treeでやろうとした
BIT使った

みたいな声が多数。前々から名前だけ知ってたBIT(Binary Indexed Tree)ですが、ついに習得するときが来たらしい。以下のスライドで勉強させて頂きました、ありがとうございます！

http://hos.ac/slides/20140319_bit.pdf

"「普通に Binary Indexed Tree を使うだけ」の部分で詰まらないようになる"、まさに今の状況ですね。

さてBITは一応実装したものの、対戦相手の決定にどう使えば良いのか全然分からん..と思っていたら、Twitterで

優先度付きキューでやった

というTweetを見かけてやっと解法に思い至りました。

解法

最善の解法がどうなのかは不明ですが、この解法では対戦相手の決定に優先度付きキューを、並べ替えの回数を求めるのにBITを使用しています。 ※説明を簡単にするため高橋くんチーム、青木くんチームの $i$ 番目のメンバーを、それぞれ $a_i, b_i$ と標記します。

まず対戦相手の決定の仕方について。 $B_i \leq B_{i+1} (1 \leq i \lt N)$ が成り立っているため、 $b_N$ の相手は、 $A_i \geq B_N$ なる $i ( 1 \leq i \leq N)$ のうち、 $i$ が最大となる $a_i$ にすれば交換回数が最小になります。 $b_{N-1}, b_{N-2}, ... , b_{1}$ についても同様に決定していけば良いです。

問題はどうやって効率的に決定を行うか。 $b_i$ ごとに $A$ を後ろから見て行って、 $A_j \geq B_i$ かつ $a_j$ がまだ誰の相手にも成っていなければ $a_j$ を $b_i$ の対戦相手に決定するのが愚直な方法ですが、これだと計算量が $O(N^2)$ になります。制約が $1\leq N \leq 10^5$ なのでこれだと絶対TLEです。(部分点は取れます)

そこでまず $(i,A_i)$ を要素とするリスト $A'$ を用意し、これを第二要素(ワザマエ)の大きい順にソートします。すると $b_N$ の対戦相手の候補は、ある $k$ が存在して、 $1 \leq i \leq k$ を満たす $A'_i$ に対応する $a_j$ となります（添字適当ですみません）。 $A'$ はワザマエ順に並んでいるので、 $B_N$ を越えるワザマエを持つものは絶対に先頭から並んでいるはずです。入力例２で考えてみると、以下のようになります。

f:id:Tawara:20151118014354p:plain ポイントは $b_{i+1}$ の対戦候補に挙がったものは $b_i$ の対戦候補にもなるということです。A'を先にソートしておくことで、対戦候補の列挙自体は $O(N)$ で済むことに成ります。

あとは対戦候補のうち一番右側に居る人を対戦相手に選べば良いんですが、これを効率的に行うために優先度付きキューを使います。対戦候補に挙がったものを全て優先度付きキューに突っ込んで番号が大きい順に並ぶようにすれば、更新が $O(logN)$ で出来ることから全体で $O(NlogN)$ で対戦相手の決定を行えます(計算量については大分適当に言ってます)。

次に交換回数の求め方について。もっかい入力例２で考えてみます。

f:id:Tawara:20151108012317p:plain

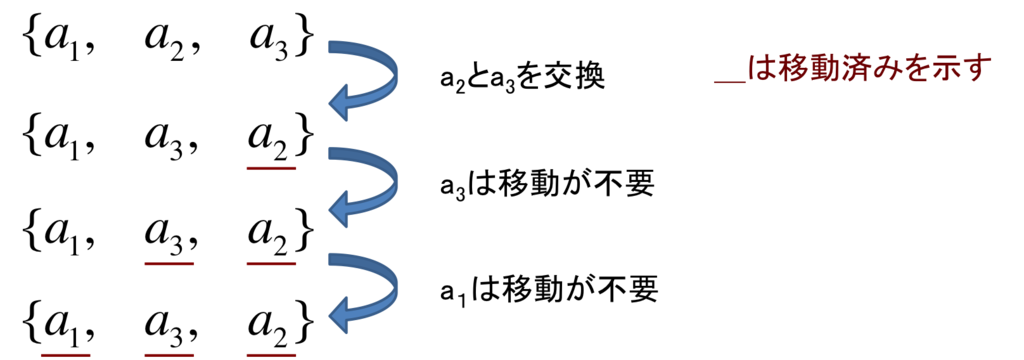
Nが小さいので例として微妙ですが、要は今から移動させる $a_i$ の右側に移動していないものが何個あるかで $a_i$ を移動させる為の交換回数が決定します。つまり、 $a_i$ を移動させる際の交換回数は $a_j$ ( $i+1 \leq j \leq N$ )のうち移動済でないものの個数です。この移動済かどうかの値を区間で効率的に管理するためにBITを使います。

実装

pythonのheapqは要素が小さいもの順に並ぶので、実際にはA'の要素は $(-i, A_i)$ としています。また、BITの区間和で求まるのは通常[1,a]の区間和ですが、今回欲しいのは[a,N]の区間和なので対応を逆にする( $a_i$ をN-iに対応させる)ことで処理しています。

from heapq import heappush,heappop
N = int(raw_input())
bit = [i&(-i) for i in xrange(N+1)]
def bit_add(a,w):
    while a <= N:
        bit[a] += w
        a += a&(-a)
def bit_sum(a):
    ret = 0
    while a > 0:
        ret += bit[a]
        a -= a&(-a)
    return ret
A = [(-i,v) for i,v in enumerate(map(int,raw_input().split()))]
A.sort(key = lambda x: x[1],reverse = True)
B = map(int,raw_input().split())
pos = cnt = 0
Q = []
for i in xrange(N):
    while pos < N and B[N-1-i] <= A[pos][1]:
        heappush(Q,A[pos])
        pos += 1
    if not Q:
        print -1
        break
    idx = N + heappop(Q)[0]
    cnt += bit_sum(idx)-1
    bit_add(idx,-1)
else:
    print cnt

終わりに

復習記事久々に書いたら何かすごい長さになってしまった。解けるのとちゃんと説明できるのは別だなあと思います。A~Gはなんとか解けましたが、H以降は厳しそう。Hは桁DPらしいのでまだ行ける気がするんですが、I以降の問題は解説から全然意味が分からなかった..。マヤノルム？知らない子ですね..

別件ですがCodeFestival通りました！もうあと一週間ですね。参加できる最初で最後の機会なので思いっきり楽しもうと思います！

2015-10-19

SRM671 Div2(Easy,Med)

いったいいつぶりの投稿だろうか..

Medで少し学ぶことがあったのでいい機会だと思って復活しました。hard時間内で解こうと意気込んでたら全然出来んかった..クマさんにいじめられる回です。

Easy (250) : BearPaints

問題文の要約

幅 $W$ マス, 高さ $H$ マスの直方体のマス目が与えられる。直方体を成すようにマスをぬるとき、 $M$ マス分のインクで最大何マスをぬることができるか？

制限

時間 : 2秒, メモリ : 256MB

制約

$1 \leq W,H \leq 10^6, 1 \leq M \leq 10^{12}$

解法

全探索をしてしまうと最悪計算量が $10^6 * 10 ^6 = 10^{12}$ かかってしまうので幅の方だけ探索を行います。塗る直方体の片方の辺の長さを $i (1 \leq i \leq W)$ に固定すると、ぬることができる直方体のマス目は

$i * H \leq M$ のとき　 $i*H$
そうでないとき　 $i*(M / i)$ (" $/$ "は小数を切り捨てる除算)

となるので、iを動かしていけば最大値が見つかります。

実装

実際の実装では幅と高さのうち小さい方を動かすようにしてます。

class BearPaints:
    def maxArea(self, W, H, M):
        l = min(W,H)
        h = max(W,H)
        return max([i*h if i*h <= M else i*(M/i) for i in xrange(1,l+1)])

Med (500) : BearDartsDiv2

問題文の超要約

長さNの自然数列 $w$ が与えられる。 $w_i * w_j * w_k = w_l (0 \leq i \lt j \lt k \lt l \lt N)$ なる $(i,j,k,l)$ の取り方は何通りあるか？

制限

時間 : 1秒, メモリ : 256MB

制約

$4 \leq N \leq 500, 1 \leq w_i \leq 10^6$

解法

もちろん、全組み合わせを確かめようとすると $_NC_4$ 通り、最悪で $_{500}C_4 = 2573031125 \fallingdotseq 2.6*10^9$ 通りあるので1秒では全探索はキツそう。ってわけでDPを使うことにしました。

DPのためのmapとしてdp1, dp2,dp3の三つを用意し、 $w$ を左から順にチェックして更新します。 $w_l (0 \leq l \lt N)$ をチェックする際に三つのマップは

dp1 : $w_i$ のとる値(key)の組み合わせ数(value) ( $0 \leq i \lt l$ )
dp2 : $w_i * w_j$ のとる値(key)の組み合わせ数(value)( $0 \leq i \lt j \lt l$ )
dp3 : $w_i * w_j * w_k$ のとる値(key)の組み合わせ数(value)( $0 \leq i \lt j \lt k \lt l$ )

という状態になっており、dp3[ $w_l$ ]の値を答えに加えたあと、dp3, dp2, dp1の順番で更新します。これなら掛け算の組み合わせがまとまるので多分行けるはず。

実装

今回は制約が厳しそうだったのでC++で実装することにしました。超シンプルに書けたので満足。

class BearDartsDiv2 {
    public:
    LL count(vector<int> w) {
        LL ans = 0, N = w.size(), wi = 0;
        map <LL, LL> dp1, dp2, dp3;
        map <LL, LL> :: iterator it;
        for(int i = 0; i < N; i++){
            wi = (LL) w[i];
            ans += dp3[wi];
            for(it = dp2.begin(); it != dp2.end(); it++) dp3[(it->first)*wi] += it->second;
            for(it = dp1.begin(); it != dp1.end(); it++) dp2[(it->first)*wi] += it->second;
            dp1[wi] += 1;
        } 
        return ans;
    }
};

だがしかし..

「hardは解けなかったけど、med綺麗に解けたから満足！」っとか言ってたら、落ちましたorz。TLEでした。行けると思ってたんですがどうやら1秒は思ったより厳しかったらしい.. しかしこの方針自体は気に入ってるのでどうにか通したい..

解法(その2)

さきほどの解法では, $w_i * w_j * w_k = w_l (0 \leq i \lt j \lt k \lt l \lt N)$ について、先に $w_i * w_j * w_k$ の組み合わせを作っておき、それと $w_l$ が一致するかどうか確かめていく方法でした。しかしこの方法では掛け算の組み合わせが爆発するらしい..

そこで少し考え方を変えてみます。 $w_i * w_j * w_k = w_l (0 \leq i \lt j \lt k \lt l \lt N)$ というのは即ち、

$w_i = w_l \div w_k \div w_j (0 \leq i \lt j \lt k \lt l \lt N , w_l \% w_k = 0, (w_l \div w_k) \% w_l = 0)$

と言い換えることが出来ます。この考え方で、 $w_l \div w_k \div w_j$ を先に作っておき、 $w_i$ と一致するか確かめるよう dp1,dp2,dp3を変更し、 $w$ を右からチェックしていきます。 $w_i (0 \leq i \lt N)$ をチェックするときの各mapの状態は、

dp1 : $w_l$ のとる値(key)の組み合わせ数(value) ( $i \lt l \lt N$ )
dp2 : $w_l \div w_k$ のとる値(key)の組み合わせ数(value)( $i \lt k \lt l \lt N$ )。ただし、 $w_l \% w_k = 0$
dp3 : $w_l \div w_k \div w_j$ のとる値(key)の組み合わせ数(value)( $i \lt j \lt k \lt l \lt N$ )。ただし、 $w_l \% w_k = 0$ かつ $(w_l \div w_k) \% w_j = 0$

となっており、dp3[ $w_i$ ]の値を答えに加えたあと、dp3, dp2, dp1の順番で更新します。最初の解法だと掛け算の取りうる値は全てmapに記録されましたが、この解法だと割り切れないものは弾かれるので計算量が大幅に減少します。

実装

実装自体はほとんど一緒です。右からチェックするのと、割り切れるかのチェックが加わっているだけなので。

class BearDartsDiv2 {
    public:
    LL count(vector<int> w) {
        LL ans = 0, N = w.size(), wi = 0;
        map <LL, LL> dp1, dp2, dp3;
        map <LL, LL> :: iterator it;
        for(int i = N-1; i >= 0; i--){
            wi = (LL) w[i];
            ans += dp3[wi];
            for(it = dp2.begin(); it != dp2.end(); it++) if ((it->first) % wi == 0) dp3[(it->first)/wi] += it->second;
            for(it = dp1.begin(); it != dp1.end(); it++) if ((it->first) % wi == 0) dp2[(it->first)/wi] += it->second;
            dp1[wi] += 1;
        } 
        return ans;
    }
};

結果

ちゃんと通りました！やったね！最初の解法だとTLEだったcaseもこの解法なら数十msぐらいで行けるという。割り算って偉大だ。

ちなみに、もしかしたらこの方針ならpythonでも行けるかも？と思ってやってみると..

class BearDartsDiv2:
    def count(self, w):
        ans = 0
        dp1 = collections.defaultdict(int)
        dp2 = collections.defaultdict(int)
        dp3 = collections.defaultdict(int)
        for wi in reversed(w):
            ans += dp3[wi]
            for k,v in dp2.iteritems():
                if k % wi == 0:
                    dp3[k/wi] += v
            for k,v in dp1.iteritems():
                if k % wi == 0:
                    dp2[k/wi] += v
            dp1[wi] += 1
        return ans

通りました！こちらも最悪ケースが数十msぐらい。割り算すげえ..

まとめ

本番ではTLEしちゃいましたが、掛け算の取りうる値の通り数をチェックするときに割り算で攻めるのはとてもいい知見だと思いました。何らかの機会に生かしたい。あと、左から $w_i*w_j$ 、右から $w_l \div w_k (w_l \% w_k = 0)$ の値を作っておいて..といった手法も出来そうな気がしますが、mapが $2N$ 個必要になるので、今回の手法の方が好きかな。 hardについては..そのうち..多分..

2015-06-24

SRM661 Div2(hard)復習

ちょっと前にSRM661 Div2のeasyとmedを復習したんですが, hardもやっと解けました.

あとこの前のTCO Round2B で無謀にもチャレンジしたせいでレートが200下がって一気に灰色まで落ちました. 泣きたい..

hard(950) : ColorfulLineGraphsDiv2

問題文のおおよその意訳

ボブは以下の２つの手順でN個の節点からなるグラフを作ろうとしている.

1からNの番号をつけた節点を用意し, それぞれの節点にはK色のうちのいずれか一色で色を塗る.
それぞれの節点i $(2\leq i \leq N)$ から, 節点iと色の異なる節点j $( j\lt i )$ に枝を張る. ただし, ボブは枝を張らないこともある.

N $(1 \leq N \leq 100)$ とK $(1 \leq K \leq 3)$ が与えられたとき, ボブが作りうるグラフの数を求め, $10^9+7$ で割った余りを答えよ.

解法

枝の張り方は色さえ決まっていたらO(N)で求められますが, そもそも色の塗り方が $K^N$ , 最悪 $3^{100}$ あるので, 塗り方ごとに枝の張り方を考えて数えるなんて事は到底無理. さてどうするか.

色々悩んだんですが, 最終的にDPになりました. 例えば, K=2として以下のようにN=2のグラフにもう一つ節点を加えてN=3のグラフを作ることを考えます.

f:id:Tawara:20150624001112p:plain

まず三つめの節点から枝を張らない場合, 好きな色の節点(赤か青)を三つ目の節点に選べるので2通り作れます. 次に三つ目の節点から枝を張る場合, 一つ目の節点に枝を張りたいなら青以外の色, すなわち赤を三つ目の節点に, 二つ目の節点に枝を張りたい場合は青を三つ目の節点に選ぶ必要があります. よって枝を張る場合も2通り作れて, 合計4通り作れます.

上のことは書いてみると結構当たり前のことなんですが, 枝を張る場合と張らない場合を分けて考えるのが一番のポイントなんじゃないかなーと思います. 三つ目の節点の色を決めてから枝を張れるかどうか考えると非常にややこしいんですが, 分けて考えてしまうととても楽です. 枝を張る先ごとに色を決めるってのが超重要.

因みに3色の場合も同様に以下のように考えられます.

f:id:Tawara:20150624003708p:plain

枝を張らない場合は3通りで, 枝を張る場合は張る先の節点以外の色を三つ目の節点の色に使えるので2*2=4通り, 合計7通りです.

もうちょっと一般的にn-1個の節点からなるグラフにn個目の節点を加えてグラフを作ることを考えると, 枝を張らない場合は単純にK通り, 張る場合は枝を張る先の節点i ( $1\leq i \leq n-1$ )ごとにn個目の節点にiと違う色すなわちK-1色のいずれかを選ぶことになるので, 作り方は

$K + (n-1)(K-1)$

通りとなります. よってボブの作りうるn個の節点からなるグラフが $a_n$ 通りだとすると, 漸化式

$a_{n+1} = a_n \lbrace K + n(K-1)\rbrace$

が成り立ちます. あとはこの式でn = 1からNまで順に求めていけば終わりです.

実装

前述の漸化式実装するだけなのでめちゃくちゃシンプルになりました.

class ColorfulLineGraphsDiv2:
    def countWays(self, N, K):
        mod = 10**9+7
        result = 1
        for i in range(N):
            result *= (K + i*(K-1)) % mod
        return result % mod

終わりに

後から聞いたんですが, Div2は制約が緩いのでここまでちゃんとやらなくても解けたらしいです(その分コードは長くなりそうですが). 逆にDiv1では制約が恐ろしいことになってて( $10^{12}$ とか), 単に漸化式作るだけでは無理だったそうな.

なにはともあれ, これでSRM661は終わりです. この調子で今までの宿題も少しずつ解いていきたい.

f:id:Tawara:20150624011117p:plain

2015-06-13

SRM661 Div2(Easy, Med)復習 —ワーシャルフロイドに惑う—

昨日の朝にあったSRM661に参加しました。

DIV1に上がってやるぜとか意気込んでたのにEasyしか解けなかった..しかも結果的にはMedはけっこう簡単だったみたいで、非常につらい。

Hardにたどり着けてないので宿題に..こんなことばっか言ってるなあ。

Easy (250) : FallingSand

(問題文のおおよその意訳)

正方形のマス目に分かれた長方形のボードが与えられ、いくつかのマスに障害物が、いくつかのマスに砂粒がある。この盤を立てたときの最終的なボードの状態を答えよ。ただし障害物は動かず、砂粒は何も無いマスにのみ落ちるものとする。(一マスに砂粒は一つしか入らない)。

これは単にシミュレーションするだけでした。stringで与えられるのがちょっとめんどくさいですね。

class FallingSand:
    def simulate(self, board):
        b = [list(s) for s in board]
        r = len(b)
        c = len(b[0])
        for i in range(c):
            for j in range(r-2,-1,-1):
                if b[j][i] == "o":
                    for k in range(j,r-1): 
                        if b[k+1][i] == ".":
                            b[k][i] = "."
                            b[k+1][i] = "o"
                            continue
                        break
        ans = tuple("".join(s) for s in b)
        return ans

Med (500) : BridgeBuildingDiv2

(問題文のおおよその意訳)

大きさがN( $2 \le N \le 11$ )の２つの節点列A,Bが与えられる。それぞれの列の隣り合う接点は辺で結ばれており、Aのi番目の節点とi+1番目の節点の間の辺の長さはa[i]、Bのi番目の節点とi+1番目の節点の間の辺の長さはb[i]である。ここで、長さ0のK本( $1 \le K \le N-1$ )の新しい辺をAの節点とBの節点の間に加えることを考える(ただし、辺を加えられるのはAのi番目の節点とBのi番目の節点(i=0,1, ... , N-1)の間のみ)。

新しい辺を加えてできたグラフについて、二節点間の最短距離のうち最大のものをグラフの直径と定義する。グラフの直径が最小になるようにK本の辺を加えたときのグラフの直径を求めよ。

f:id:Tawara:20150613010359p:plain

全点対距離..いつか勉強したワーシャルフロイドを使うときが来た！と、思ったのですが、N本からK本を選んで新しい辺を加え、そこから計算することを考えると、計算量は $_NC_k \times (2N)^3$ 、N = 11, K = 6のときなら $_{11}C_6 \times (22)^3 = 4919376 \fallingdotseq 5.0 \times 10^6$ 。ああ、pythonあかんやつやんこれ..

それでC++で実装しようとしたんですけど、組み合わせの列挙どうしたら良いんやってあーだこーだしてて終了致しましたorzやっぱ普段からやってないと駄目ですね。

どうやら全点についてダイクストラ法を用いると、計算量が $_NC_k \times (2N+(2(N-1)+K)) \log2N$ ぐらいなんでそれで行けたっぽい..のですが、やっぱpythonでもワーシャルフロイドで通したい！ってことで考えてみました。

ワーシャルフロイドでは、ある中継点kを考えたときの(i-k間の距離＋ k-j間の距離)と現時点のi-j間の距離の小さい方をi-j間の距離とするのを繰り返すことで全節点対の最短距離を求めます。ここで、通常は中継点に全節点を用います。今回はAの節点を0, .., N-1、Bの節点をN, ..., 2N-1 として

for k in range(2*N):
        for i in range(2*N):
                for j in range(2*N):
                        d[i][j] = min(d[i][j], d[i][k]+d[k][j])

をK本の新しい辺の加え方ごとにやることになります。ただこれでは計算量がよろしくない。

よくよく考えると、新しい辺を加えたときにある二節点間の最短距離が更新されるなら、その経路は絶対にいずれかの新しい辺を通ることが分かります。となれば、まず節点列A,Bそれぞれの中で全節点対の最短距離を求めておいた後に、新しく加えた辺の両端の節点のみを中継点としてワーシャルフロイドを実行すればいけそう。

for k in inter: #interはいずれかの新しい辺の両端の節点
        for i in range(2*N):
                for j in range(2*N): 
                        d[i][j] = min(d[i][j],d[i][k]+d[k][j])

というわけで以下のようになりました。

import itertools, copy

MAX = 1000
class BridgeBuildingDiv2:
    def minDiameter(self, a, b, K):
        N = len(a)+1
        d = [[MAX for j in range(2*N)] for i in range(2*N)]

        ## 距離の初期化
        for i in range(2*N):
            d[i][i] = 0

        for i in range(N-1):
            d[i][i+1] = d[i+1][i] = a[i]
            d[N+i][N+i+1] = d[N+i+1][N+i] = b[i]

        ## 節点列A,Bごとに全節点対の最短距離を計算
        for i in range(N-2):
            for j in range(i+2,N):
                d[i][j] = d[j][i] = d[i][j-1] + d[j-1][j]
                d[N+i][N+j] = d[N+j][N+i] = d[N+i][N+j-1] + d[N+j-1][N+j]

        ans = MAX
        ## 新しい辺の加え方ごとにワーシャルフロイドを行う
        for bridge in itertools.combinations(range(N),K):
            tmpd = copy.deepcopy(d)
            for k in bridge:
                tmpd[k][N+k] = tmpd[N+k][k] = 0
            ## 中継点は新しい辺の両端のみ
            inter = list(bridge) + [N+i for i in bridge]
            for k in inter:
                for i in range(2*N):
                    for j in range(2*N): 
                        tmpd[i][j] = min(tmpd[i][j],tmpd[i][k]+tmpd[k][j])

            ans = min(ans, max(max(tmpd[i]) for i in range(2*N)))
        return ans

最悪計算量はN=11, K=6のときの $_{11}C_6 \times (2\times 6) \times (22)^2 = 2683296 \fallingdotseq 2.7 \times 10^6$ 。え？あんまり変わってない？いやpythonは $10^6$ の世界入るととってもシビアなんでちょっとの削減がめっちゃ大事です。

さあシステムテストだ！

f:id:Tawara:20150613123942p:plain

やりました！ワーシャルフロイドは見た目より速いって聞いてたけど $2.7 \times 10^6$ でも通るもんなんですねえ。テストケースに一番最悪のケースが無いのもありますが、手元ではいけてました。いやー満足した！

かに見えた..

ところで、通常のワーシャルフロイドだとシステムテストではどれくらいかかるのでしょうか？まあTLEになるんでしょうけど気になるからやってみましょう！

f:id:Tawara:20150613123946p:plain

って通るんかーい！！僕のここまでの苦労は何だったんでしょうか... システムテストの最悪ケースは N= 11, K=7なので、計算量は $_{11}C_7 \times (22)^3 = 3513840 \fallingdotseq 3.5 \times 10^6$ 、まあたしかに雑魚いから仕方ないか？

と思って、ワーシャルフロイドで解いてるpythonistaの皆さんに手当たり次第N=11, K=6でchallengeしたんですが弾かれちゃいました。色々考えたのに結局単純なワーシャルフロイドで通るとかつらい..

終わりに

結局僕の空回りでしたが、グラフの連結部だけに注目するってのはまた使うことになりそうな気がします。どっかで今回の考察が活きると信じよう。

Hardも解きたいし、C++での実装と全点ダイクストラも一応やっときたい、というところで今回は終わりです。あと全く関係ないですがCodeforces #307が全然解けなくて泣きそうでした。